More about full diversity rotations

We briefly explain how lattices can be constructed using algebraic number theory. We assume some basic knowledge of algebraic number theory (for an introduction to the topic, see [OV04]). We first consider a number field, that is a field extension of Q, that we denote by K. Assume its degree over Q is n. Then, we consider OK, its ring of integers, which furthermore possesses a basis B={ w1,...,wn} over Z. Namely, every element x of OK can be written as a integral linear combination of the wi, i=1...n. Suppose now that K is totally real, that is, it has n real embeddings σi, i=1...n, into C. We call the canonical embedding of K into Rn the following map: σ=(σ1,...,σn). By applying the canonical embedding to every element of the basis B, we get a matrix, that can be shown to be the generator matrix of a lattice. This construction can be generalized by considering not only a basis of OK, but more generally a basis of an ideal of OK. Note that the algebraic construction works for number fields of any signature (r1,r2) and yields a diversity L=r1+r2, [BV98]. Using totally real number fields  (r1=n and r2=0), we guarantee full diversity L=n.
In order to build a particular lattice of dimension n, we have to choose a number field K of degree n and an ideal I of OK. This is the procedure we are following for building Zn lattices. Note that in some cases, a twisting element may be added to get the desired lattice [BOV04]. We consider several constructions to build Zn lattices in all dimensions.
  1. The cyclotomic construction [BOV04]: we consider a number field K with primitive element 2cos(2π/n), where n=(p-1)/2 for p a prime number. Then we take the whole ring of integers, but we introduce a twisting element α = 2-2cos(2π/n).
  2. The cyclic construction  [BOV04]: we consider a cyclic number field K, that is a field whose Galois group is cyclic. It can be described by saying in which cyclotomic field it is embedded: K ⊂ Q(exp(2πi/m)). The ideal we take is the square root of the codifferent of K.
  3. Kruskemper's construction  [OB03]: this is an algorithm which given a Gram matrix of a lattice computes its generator matrix, as the embeddings of a number field. The number field is given by its minimal polynomial.
  4. Mixed construction [BOV04]: this method allows to take two lattices of dimensions n and m and combine them to get a lattice in dimension nm.
  5. Other types of constructions have been found for dimensions multiples of 8  [DAB02].
BACK TO TABLE

 

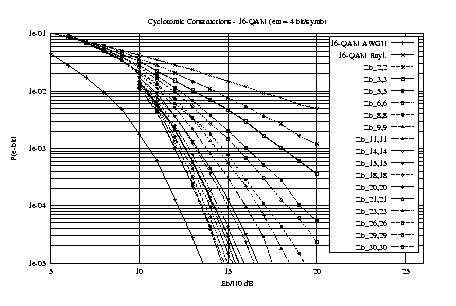
Some Bit Error probability curves

The following figures show the performance of rotated Zn lattice constellations over the independent Rayleigh fading channel for two different spectral efficiencies: 1 bit per dimension (as QPSK) and 2 bits per dimension (as 16-QAM). As the dimension (hence diversity) increases, performance approaches the AWGN channel performance (lowest curve).
Figure QPSK
Figure 16-QAM

 
 
 
 
 
 

References

[O05]  F. Oggier, Algebraic methods for channel coding, Ph.D. Thesis, EPFL, 2005.
[OV04]  F. Oggier and E. Viterbo, "Algebraic number theory and code design for Rayleigh fading channels," 
 in Foundations and Trends in Communications and Information Theory, vol. 1, pp. 333-415, 2004.
[BOV04]  E. Bayer-Fluckiger, F. Oggier, E. Viterbo, "New Algebraic Constructions of Rotated Z^n-Lattice Constellations for the Rayleigh Fading Channel,"
 IEEE Transactions on Information Theory, vol. 50, n. 4,  pp. 702-714, Apr. 2004.
[OB03]  F. Oggier, E.  Bayer-Fluckiger, "Best rotated cubic lattice constellations for the Rayleigh fading channel,"
 Proceedings of the IEEE International Symposium on Information Theory, Yokohama, Japan, 2003.
[DAB02]  M.O. Damen, K. Abed-Meriam, J.-C. Belfiore, "Diagonal algebraic space-time block codes,"
 IEEE Transactions on Information Theory, vol. 48,  pp. 628-636, Mar. 2002.
[BV98]  J. Boutros and E. Viterbo: "Signal Space Diversity: a power and bandwidth efficient diversity technique for the Rayleigh fading channel,"
 IEEE Transactions on Information Theory, vol. 44, n. 4, pp.  1453-1467, July 1998.
[GBB97]
  X. Giraud, E. Boutillon, and J.C. Belfiore, "Algebraic tools to build modulation schemes for fading channels,"
 IEEE Transactions on Information Theory, vol. 43, n. 3, pp.  938-952, May 1997.
[BVRB96]
  J. Boutros, E. Viterbo, C. Rastello, and  Belfiore, J.-C., "Good lattice constellations for both Rayleigh fading and Gaussian channels"
 IEEE Transactions on Information Theory, vol. 42, n. 2,  pp. 502-518, March 1996.
[GBB93]
  X. Giraud, K. Boulle, and J.-C. Belfiore, "Constellations Designed for the Rayleigh Fading Channel,"
 IEEE International Symposium on Information Theory, January 17-22, 1993, p. 342.
[BB92]
  K. Boulle and J.-C. Belfiore: "Modulation schemes designed for the Rayleigh channel,"
 Conference on Information Sciences and Systems, Princeton, 1992, pp. 288-293.

 
 
BACK TO TABLE

 
 
 
 
Last modified 16/3/2005 by Frederique Oggier and Emanuele Viterbo ©